| Basic formulas | ||
|---|---|---|
| <math></math> |  | |
| 10 | <math> <mn>10</mn> </math> | 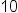 |
| x | <math> <mi>x</mi> </math> | 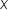 |
| 4x | <math> <mn>4</mn> <mi>x</mi> </math> | 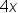 |
| \sin x (1) | <math> <mi mathvariant="normal">sin</mi> <mi>x</mi> </math> | 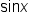 |
| 4+x | <math> <mn>4</mn> <mo>+</mo> <mi>x</mi> </math> | 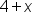 |
| 3\leq8.3 | <math> <mn>3</mn> <mo>≤</mo> <mn>8</mn> <mo>.</mo> <mn>3</mn> </math> | 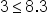 |
| \frac12 | <math> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> </math> | 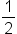 |
| \frac24 (1) | <math> <mfrac bevelled="true"> <mn>2</mn> <mn>4</mn> </mfrac> </math> | 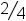 |
| \frac{-x}2 | <math> <mfrac> <mrow> <mo>-</mo> <mi>x</mi> </mrow> <mn>2</mn> </mfrac> </math> | 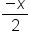 |
| x^2-1 | <math> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>-</mo> <mn>1</mn> </math> | 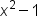 |
| A_j | <math> <msub> <mi>A</mi> <mi>j</mi> </msub> </math> | 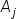 |
| \sqrt x | <math> <msqrt> <mi>x</mi> </msqrt> </math> | 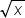 |
| \sqrt[3]8=2 | <math> <mroot> <mn>8</mn> <mn>3</mn> </mroot> <mo>=</mo> <mn>2</mn> </math> | 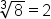 |
| \left(1,2\right) | <math> <mfenced> <mrow> <mn>1</mn> <mo>,</mo> <mn>2</mn> </mrow> </mfenced> </math> | 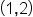 |
| \left|x-1\right|<\varepsilon | <math> <mfenced close="|" open="|"> <mrow> <mi>x</mi> <mo>-</mo> <mn>1</mn> </mrow> </mfenced> <mo><</mo> <mi>ε</mi> </math> | 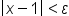 |
| \pm\infty | <math> <mo>±</mo> <mo>∞</mo> </math> | 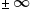 |
| \varnothing=\{\;\} | <math> <mo>∅</mo> <mo>=</mo> <mo>{</mo> <mo> </mo> <mo>}</mo> </math> | 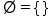 |
| A\cap B\cup C | <math> <mi>A</mi> <mo>∩</mo> <mi>B</mi> <mo>∪</mo> <mi>C</mi> </math> | 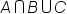 |
| a_1\times a_2 | <math> <msub> <mi>a</mi> <mn>1</mn> </msub> <mo>×</mo> <msub> <mi>a</mi> <mn>2</mn> </msub> </math> | 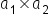 |
| 4\in\left\{2,4,6\right\} | <math> <mn>4</mn> <mo>∈</mo> <mfenced close="}" open="{"> <mrow> <mn>2</mn> <mo>,</mo> <mn>4</mn> <mo>,</mo> <mn>6</mn> </mrow> </mfenced> </math> | 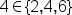 |
| \left\{\frac12\left(x^4-3\right)\right \}^\frac12 | <math> <msup> <mfenced close="}" open="{"> <mrow> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> <mfenced> <mrow> <msup> <mi>x</mi> <mn>4</mn> </msup> <mo>-</mo> <mn>3</mn> </mrow> </mfenced> </mrow> </mfenced> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> </msup> </math> | 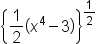 |
| Format | ||
| \mathbf z=\mathbf u+\mathbf v | <math> <mi mathvariant="bold">z</mi> <mo>=</mo> <mi mathvariant="bold">u</mi> <mo>+</mo> <mi mathvariant="bold">v</mi> </math> | 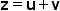 |
| 1{\color[rgb]{1.0, 0.0, 0.0}+}2{ \color[rgb]{0.0, 0.0, 1.0}=}3 | <math> <mn>1</mn> <mo mathcolor="#FF0000">+</mo> <mn>2</mn> <mo mathcolor="#0000FF">=</mo> <mn>3</mn> </math> | 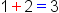 |
| \mathbf4\mathrm x+\mathbf2\mathrm y | <math> <mn mathvariant="bold">4</mn> <mi mathvariant="normal">x</mi> <mo>+</mo> <mn mathvariant="bold">2</mn> <mi mathvariant="normal">y</mi> </math> | 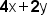 |
| \style{font-size:24px}{{ \color[rgb]{0.0, 0.5, 0.0}\mathit2}{ \color[rgb]{0.0, 0.5, 0.0}-}{ \color[rgb]{0.0, 0.5, 0.0}\frac{ \mathit1}{\mathit3}}} (1) | <math style="font-size:24px"> <mn mathcolor="#007F00" mathvariant="italic">2</mn> <mo mathcolor="#007F00">-</mo> <mfrac mathcolor="#007F00"> <mn mathvariant="italic">1</mn> <mn mathvariant="italic">3</mn> </mfrac> </math> | 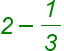 |
| \style{font-family:'Times New Roman'}{f'(x)={ \textstyle\frac12}x^2} | <math style="font-family:'Times New Roman'"> <mi>f</mi> <mo>'</mo> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mo>=</mo> <mstyle displaystyle="false"> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> </mstyle> <msup> <mi>x</mi> <mn>2</mn> </msup> </math> | 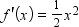 |
| \style{font-family:'Courier New'}{a^2-b^2} | <math style="font-family:'Courier New'"> <msup> <mi>a</mi> <mn>2</mn> </msup> <mo>-</mo> <msup> <mi>b</mi> <mn>2</mn> </msup> </math> | 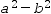 |
| Arrows | ||
| a\Rightarrow b | <math> <mi>a</mi> <mo>⇒</mo> <mi>b</mi> </math> | 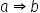 |
| x\overset{\text{maps to}}\mapsto y | <math> <mi>x</mi> <mover> <mo>↦</mo> <mtext>maps to</mtext> </mover> <mi>y</mi> </math> | 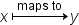 |
| a_1\times\cdots\times a_n | <math> <msub> <mi>a</mi> <mn>1</mn> </msub> <mo>×</mo> <mo>⋯</mo> <mo>×</mo> <msub> <mi>a</mi> <mi>n</mi> </msub> </math> |  |
| \overset\rightharpoonup{AB}=-\overset \rightharpoonup{BA} | <math> <mover> <mrow> <mi>A</mi> <mi>B</mi> </mrow> <mo>⇀</mo> </mover> <mo>=</mo> <mo>-</mo> <mover> <mrow> <mi>B</mi> <mi>A</mi> </mrow> <mo>⇀</mo> </mover> </math> | 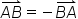 |
| Symbols | ||
| 1+2\times3-4\div5 | <math> <mn>1</mn> <mo>+</mo> <mn>2</mn> <mo>×</mo> <mn>3</mn> <mo>-</mo> <mn>4</mn> <mo>÷</mo> <mn>5</mn> </math> | 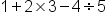 |
| 8\pm0.001 | <math> <mn>8</mn> <mo>±</mo> <mn>0</mn> <mo>.</mo> <mn>001</mn> </math> | 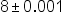 |
| f\ast(x) | <math> <mi>f</mi> <mo>*</mo> <mo>(</mo> <mi>x</mi> <mo>)</mo> </math> | 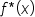 |
| (f\circ g)(x\cdot y) | <math> <mo>(</mo> <mi>f</mi> <mo>∘</mo> <mi>g</mi> <mo>)</mo> <mo>(</mo> <mi>x</mi> <mo>·</mo> <mi>y</mi> <mo>)</mo> </math> | 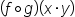 |
| 2pr^2 | <math> <mn>2</mn> <mi>p</mi> <msup> <mi>r</mi> <mn>2</mn> </msup> </math> | 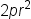 |
| 15^\circ30'60'' | <math> <mn>15</mn> <mo>°</mo> <mn>30</mn> <mo>'</mo> <mn>60</mn> <mo>'</mo> <mo>'</mo> </math> | 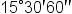 |
| f'(x)g(x)+f(x)g'(x) | <math> <mi>f</mi> <mo>'</mo> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mi>g</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mo>+</mo> <mi>f</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mi>g</mi> <mo>'</mo> <mo>(</mo> <mi>x</mi> <mo>)</mo> </math> | 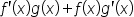 |
| x+1=1-x | <math> <mi>x</mi> <mo>+</mo> <mn>1</mn> <mo>=</mo> <mn>1</mn> <mo>-</mo> <mi>x</mi> </math> | 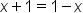 |
| A\equiv B | <math> <mi>A</mi> <mo>≡</mo> <mi>B</mi> </math> | 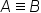 |
| 4.99\sim5 | <math> <mn>4</mn> <mo>.</mo> <mn>99</mn> <mo>∼</mo> <mn>5</mn> </math> | 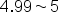 |
| \pi\approx3.1415 | <math> <mi>π</mi> <mo>≈</mo> <mn>3</mn> <mo>.</mo> <mn>1415</mn> </math> | 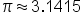 |
| 0\leq x,\;0\leqslant x | <math> <mn>0</mn> <mo>≤</mo> <mi>x</mi> <mo>,</mo> <mo> </mo> <mn>0</mn> <mo>⩽</mo> <mi>x</mi> </math> | 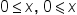 |
| 5\lneq6 | <math> <mn>5</mn> <mo>⪇</mo> <mn>6</mn> </math> | 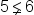 |
| x\in A\cap B | <math> <mi>x</mi> <mo>∈</mo> <mi>A</mi> <mo>∩</mo> <mi>B</mi> </math> | 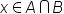 |
| \{2,4\}\subset\{1,2,3,4\} | <math> <mo>{</mo> <mn>2</mn> <mo>,</mo> <mn>4</mn> <mo>}</mo> <mo>⊂</mo> <mo>{</mo> <mn>1</mn> <mo>,</mo> <mn>2</mn> <mo>,</mo> <mn>3</mn> <mo>,</mo> <mn>4</mn> <mo>}</mo> </math> | 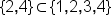 |
| \forall\varepsilon\exists\delta | <math> <mo>∀</mo> <mi>ε</mi> <mo>∃</mo> <mi>δ</mi> </math> | 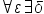 |
| \neg p\vee p | <math> <mo>¬</mo> <mi>p</mi> <mo>∨</mo> <mi>p</mi> </math> | 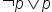 |
| (a\vee b)\wedge(c\vee d) | <math> <mo>(</mo> <mi>a</mi> <mo>∨</mo> <mi>b</mi> <mo>)</mo> <mo>∧</mo> <mo>(</mo> <mi>c</mi> <mo>∨</mo> <mi>d</mi> <mo>)</mo> </math> | 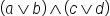 |
| \angle a | <math> <mo>∠</mo> <mi>a</mi> </math> | 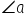 |
| r\parallel s | <math> <mi>r</mi> <mo>∥</mo> <mi>s</mi> </math> | 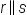 |
| r\perp s | <math> <mi>r</mi> <mo>⊥</mo> <mi>s</mi> </math> | 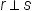 |
| 3\in\mathbb{N} | <math> <mn>3</mn> <mo>∈</mo> <mi mathvariant="normal">ℕ</mi> </math> | 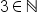 |
| \pi\in\mathbb{R}\setminus\mathbb{Q} | <math> <mi>π</mi> <mo>∈</mo> <mi mathvariant="normal">ℝ</mi> <mo>∖</mo> <mi mathvariant="normal">ℚ</mi> </math> | 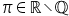 |
| \Re(4+3i)=4 | <math> <mo>ℜ</mo> <mo>(</mo> <mn>4</mn> <mo>+</mo> <mn>3</mn> <mi>i</mi> <mo>)</mo> <mo>=</mo> <mn>4</mn> </math> | 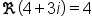 |
| error: Error converting from MathML to LaTeX (1) | <math> <mi mathvariant="double-struck">D</mi> <mo> </mo> <mo>=</mo> <mo> </mo> <mo>{</mo> <mo> </mo> <mi>z</mi> <mo>∈</mo> <mi mathvariant="normal">ℂ</mi> <mo> </mo> <mo> </mo> <mo>:</mo> <mo> </mo> <mo> </mo> <mo>|</mo> <mi>z</mi> <mo>|</mo> <mo><</mo> <mn>1</mn> <mo> </mo> <mo>}</mo> </math> | 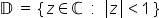 |
| error: Error converting from MathML to LaTeX (1) | <math> <msub> <mi mathvariant="double-struck">A</mi> <mi mathvariant="normal">ℚ</mi> </msub> <mo>=</mo> <mi mathvariant="normal">ℚ</mi> <mo> </mo> <msub> <mo>⊗</mo> <mi mathvariant="normal">ℤ</mi> </msub> <mo> </mo> <msub> <mi mathvariant="double-struck">A</mi> <mi mathvariant="normal">ℤ</mi> </msub> </math> | 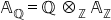 |
| \mathcal H=\sum_i{\dot q}_i\frac{ \partial\mathcal L}{\partial{\dot q}_i}- \mathcal L | <math> <mi mathvariant="script">H</mi> <mo>=</mo> <munder> <mo>∑</mo> <mi>i</mi> </munder> <msub> <mover> <mi>q</mi> <mo>˙</mo> </mover> <mi>i</mi> </msub> <mfrac> <mrow> <mo>∂</mo> <mi mathvariant="script">L</mi> </mrow> <mrow> <mo>∂</mo> <msub> <mover> <mi>q</mi> <mo>˙</mo> </mover> <mi>i</mi> </msub> </mrow> </mfrac> <mo>-</mo> <mi mathvariant="script">L</mi> </math> | 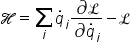 |
| {\mathcal R}_{\mathcal Q}\;\cong\;T_{ \mathcal Q} | <math> <msub> <mi mathvariant="script">R</mi> <mi mathvariant="script">Q</mi> </msub> <mo> </mo> <mo>≅</mo> <mo> </mo> <msub> <mi>T</mi> <mi mathvariant="script">Q</mi> </msub> </math> | 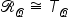 |
| \mathfrak p\;\supset\;\mathfrak{ab}\; \Rightarrow\mathfrak p\supset\mathfrak a \;\vee\;\mathfrak p\;\supset\mathfrak b | <math> <mi mathvariant="fraktur">p</mi> <mo> </mo> <mo>⊃</mo> <mo> </mo> <mi mathvariant="fraktur">ab</mi> <mo> </mo> <mo>⇒</mo> <mi mathvariant="fraktur">p</mi> <mo>⊃</mo> <mi mathvariant="fraktur">a</mi> <mo> </mo> <mo>∨</mo> <mo> </mo> <mi mathvariant="fraktur">p</mi> <mo> </mo> <mo>⊃</mo> <mi mathvariant="fraktur">b</mi> </math> | 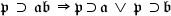 |
| \mathcal B=\{B_\alpha\in\mathcal T\, \vert\,U=\bigcup B_\alpha\forall U\in \mathcal T\} | <math> <mi mathvariant="script">B</mi> <mo>=</mo> <mo>{</mo> <msub> <mi>B</mi> <mi>α</mi> </msub> <mo>∈</mo> <mi mathvariant="script">T</mi> <mo> </mo> <mo>|</mo> <mo> </mo> <mi>U</mi> <mo>=</mo> <mo largeop="true">∪</mo> <msub> <mi>B</mi> <mi>α</mi> </msub> <mo>∀</mo> <mi>U</mi> <mo>∈</mo> <mi mathvariant="script">T</mi> <mo>}</mo> </math> | 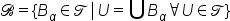 |
| A\oplus B | <math> <mi>A</mi> <mo>⊕</mo> <mi>B</mi> </math> | 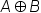 |
| i\leftarrow i+1 | <math> <mi>i</mi> <mo>←</mo> <mi>i</mi> <mo>+</mo> <mn>1</mn> </math> | 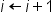 |
| x\mapsto x^2+1 | <math> <mi>x</mi> <mo>↦</mo> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>+</mo> <mn>1</mn> </math> | 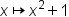 |
| x<3\wedge x\Rightarrow-2\Rightarrow x \leqslant-2 | <math> <mi>x</mi> <mo><</mo> <mn>3</mn> <mo>∧</mo> <mi>x</mi> <mo>⇒</mo> <mo>-</mo> <mn>2</mn> <mo>⇒</mo> <mi>x</mi> <mo>⩽</mo> <mo>-</mo> <mn>2</mn> </math> | 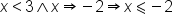 |
| \square\neq\bigcirc | <math> <mo>□</mo> <mo>≠</mo> <mo>○</mo> </math> | 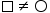 |
| a\nparallel b,\;A\not\ni x | <math> <mi>a</mi> <mo>∦</mo> <mi>b</mi> <mo>,</mo> <mo> </mo> <mi>A</mi> <mo>∌</mo> <mi>x</mi> </math> | 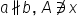 |
| Greek letters | ||
| \cos(\alpha\pm\beta)=\cos\alpha\cos\beta \mp\sin\alpha\sin\beta (1) | <math> <mi mathvariant="normal">cos</mi> <mo>(</mo> <mi>α</mi> <mo>±</mo> <mi>β</mi> <mo>)</mo> <mo>=</mo> <mi mathvariant="normal">cos</mi> <mi>α</mi> <mi mathvariant="normal">cos</mi> <mi>β</mi> <mo>∓</mo> <mi mathvariant="normal">sin</mi> <mi>α</mi> <mi mathvariant="normal">sin</mi> <mi>β</mi> </math> | 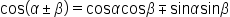 |
| \sin(\theta+\frac\pi2)=\cos\theta (1) | <math> <mi mathvariant="normal">sin</mi> <mo>(</mo> <mi>θ</mi> <mo>+</mo> <mfrac> <mi>π</mi> <mn>2</mn> </mfrac> <mo>)</mo> <mo>=</mo> <mi mathvariant="normal">cos</mi> <mi>θ</mi> </math> | 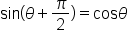 |
| \mathrm\Omega=\frac{\mathrm V}{ \mathrm A} | <math> <mi mathvariant="normal">Ω</mi> <mo>=</mo> <mfrac> <mi mathvariant="normal">V</mi> <mi mathvariant="normal">A</mi> </mfrac> </math> | 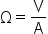 |
| \varphi(x)+\psi(y)+\xi(z) | <math> <mi>φ</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mo>+</mo> <mi>ψ</mi> <mo>(</mo> <mi>y</mi> <mo>)</mo> <mo>+</mo> <mi>ξ</mi> <mo>(</mo> <mi>z</mi> <mo>)</mo> </math> | 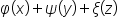 |
| Matrices | ||
| \begin{bmatrix}1\\2\end{bmatrix} | <math> <mfenced close="]" open="["> <mtable> <mtr> <mtd> <mn>1</mn> </mtd> </mtr> <mtr> <mtd> <mn>2</mn> </mtd> </mtr> </mtable> </mfenced> </math> | 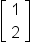 |
| \begin{pmatrix}x\\y\end{pmatrix} | <math> <mfenced> <mtable> <mtr> <mtd> <mi>x</mi> </mtd> </mtr> <mtr> <mtd> <mi>y</mi> </mtd> </mtr> </mtable> </mfenced> </math> | 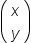 |
| \begin{pmatrix}1&\;&\;\\\;&1&\;\\\;&\;&1 \end{pmatrix} | <math> <mfenced> <mtable> <mtr> <mtd> <mn>1</mn> </mtd> <mtd> <mo> </mo> </mtd> <mtd> <mo> </mo> </mtd> </mtr> <mtr> <mtd> <mo> </mo> </mtd> <mtd> <mn>1</mn> </mtd> <mtd> <mo> </mo> </mtd> </mtr> <mtr> <mtd> <mo> </mo> </mtd> <mtd> <mo> </mo> </mtd> <mtd> <mn>1</mn> </mtd> </mtr> </mtable> </mfenced> </math> | 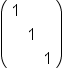 |
| \begin{vmatrix}\sin(x)&\cos(x)\\- \cos(x)&\sin(x)\end{vmatrix}=1 (1) | <math> <mfenced close="|" open="|"> <mtable> <mtr> <mtd> <mi mathvariant="normal">sin</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </mtd> <mtd> <mi mathvariant="normal">cos</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </mtd> </mtr> <mtr> <mtd> <mo>-</mo> <mi mathvariant="normal">cos</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </mtd> <mtd> <mi mathvariant="normal">sin</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </mtd> </mtr> </mtable> </mfenced> <mo>=</mo> <mn>1</mn> </math> | 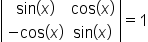 |
| \left\{\begin{array}{c}x+1\\x-1 \end{array}\right. | <math> <mfenced close="" open="{"> <mtable> <mtr> <mtd> <mi>x</mi> <mo>+</mo> <mn>1</mn> </mtd> </mtr> <mtr> <mtd> <mi>x</mi> <mo>-</mo> <mn>1</mn> </mtd> </mtr> </mtable> </mfenced> </math> | 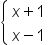 |
| f(x)=\left\{\begin{array}{lc}x,& \text{if }x\leqslant0\\\sin(x),& \text{if }x>0\end{array}\right. (1) | <math> <mi>f</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mo>=</mo> <mfenced close="" open="{"> <mtable columnalign="left" columnspacing="1.4ex"> <mtr> <mtd> <mi>x</mi> <mo>,</mo> </mtd> <mtd> <mtext>if </mtext> <mi>x</mi> <mo>⩽</mo> <mn>0</mn> </mtd> </mtr> <mtr> <mtd> <mi mathvariant="normal">sin</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> <mo>,</mo> </mtd> <mtd> <mtext>if </mtext> <mi>x</mi> <mo>></mo> <mn>0</mn> </mtd> </mtr> </mtable> </mfenced> </math> | 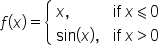 |
| \begin{array}{rcl}x^5+1&=&x^4-y\\x&=&{ \textstyle\frac12}y+3\end{array} (1) | <math> <mtable columnalign="right center left" columnspacing="2px"> <mtr> <mtd> <msup> <mi>x</mi> <mn>5</mn> </msup> <mo>+</mo> <mn>1</mn> </mtd> <mtd> <mo>=</mo> </mtd> <mtd> <msup> <mi>x</mi> <mn>4</mn> </msup> <mo>-</mo> <mi>y</mi> </mtd> </mtr> <mtr> <mtd> <mi>x</mi> </mtd> <mtd> <mo>=</mo> </mtd> <mtd> <mstyle displaystyle="false"> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> </mstyle> <mi>y</mi> <mo>+</mo> <mn>3</mn> </mtd> </mtr> </mtable> </math> | 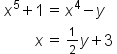 |
| \begin{array}{rcl}(2+3)^2&=&(5)^2 \\\;&=&25\end{array} (1) | <math> <mtable columnalign="right center left" columnspacing="2px"> <mtr> <mtd> <mo>(</mo> <mn>2</mn> <mo>+</mo> <mn>3</mn> <msup> <mo>)</mo> <mn>2</mn> </msup> </mtd> <mtd> <mo>=</mo> </mtd> <mtd> <mo>(</mo> <mn>5</mn> <msup> <mo>)</mo> <mn>2</mn> </msup> </mtd> </mtr> <mtr> <mtd> <mo> </mo> </mtd> <mtd> <mo>=</mo> </mtd> <mtd> <mn>25</mn> </mtd> </mtr> </mtable> </math> | 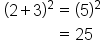 |
| Script and layout | ||
| {\textstyle\frac12}\;5 (1) | <math> <mstyle displaystyle="false"> <mfrac bevelled="true"> <mn>1</mn> <mn>2</mn> </mfrac> </mstyle> <mo> </mo> <mn>5</mn> </math> | 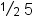 |
| 3+\frac1{7+\frac1{...}} | <math> <mn>3</mn> <mo>+</mo> <mfrac> <mn>1</mn> <mrow> <mn>7</mn> <mo>+</mo> <mfrac> <mn>1</mn> <mrow> <mo>.</mo> <mo>.</mo> <mo>.</mo> </mrow> </mfrac> </mrow> </mfrac> </math> | 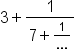 |
| \sqrt{1-x} | <math> <msqrt> <mn>1</mn> <mo>-</mo> <mi>x</mi> </msqrt> </math> | 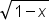 |
| \sqrt[3]2 | <math> <mroot> <mn>2</mn> <mn>3</mn> </mroot> </math> | 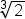 |
| \sqrt[n]{x^n+y^n} | <math> <mroot> <mrow> <msup> <mi>x</mi> <mi>n</mi> </msup> <mo>+</mo> <msup> <mi>y</mi> <mi>n</mi> </msup> </mrow> <mi>n</mi> </mroot> </math> | 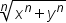 |
| \sqrt[n+1]a | <math> <mroot> <mi>a</mi> <mrow> <mi>n</mi> <mo>+</mo> <mn>1</mn> </mrow> </mroot> </math> | 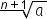 |
| (\mathrm{OH})_4^- (1) | <math> <mo>(</mo> <mi mathvariant="normal">OH</mi> <msubsup> <mo>)</mo> <mn>4</mn> <mo>-</mo> </msubsup> </math> | 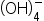 |
| {}_{92}^{235}\mathrm U | <math> <mmultiscripts> <mi mathvariant="normal">U</mi> <mprescripts></mprescripts> <mn>92</mn> <mn>235</mn> </mmultiscripts> </math> | 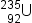 |
| (AB)_i^j=A_i^kB_k^j | <math> <mo>(</mo> <mi>A</mi> <mi>B</mi> <msubsup> <mo>)</mo> <mi>i</mi> <mi>j</mi> </msubsup> <mo>=</mo> <msubsup> <mi>A</mi> <mi>i</mi> <mi>k</mi> </msubsup> <msubsup> <mi>B</mi> <mi>k</mi> <mi>j</mi> </msubsup> </math> | 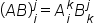 |
| \mathrm{Zn}+2\mathrm H^+\rightarrow \mathrm{Zn}^{2+}+{\mathrm H}_2 (1) | <math> <mi mathvariant="normal">Zn</mi> <mo>+</mo> <mn>2</mn> <msup> <mi mathvariant="normal">H</mi> <mo>+</mo> </msup> <mo>→</mo> <msup> <mi mathvariant="normal">Zn</mi> <mrow> <mn>2</mn> <mo>+</mo> </mrow> </msup> <mo>+</mo> <msub> <mi mathvariant="normal">H</mi> <mn>2</mn> </msub> </math> | 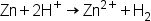 |
| \overset8{3+5} | <math> <mover> <mrow> <mn>3</mn> <mo>+</mo> <mn>5</mn> </mrow> <mn>8</mn> </mover> </math> | 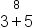 |
| \underset{(2\;\mathrm{degree})}{3x^2-2} (1) | <math> <munder> <mrow> <mn>3</mn> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>-</mo> <mn>2</mn> </mrow> <mrow> <mo>(</mo> <mn>2</mn> <mo> </mo> <mi mathvariant="normal">degree</mi> <mo>)</mo> </mrow> </munder> </math> | 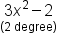 |
| \underbrace{1+2}_3 | <math> <munder> <munder> <mrow> <mn>1</mn> <mo>+</mo> <mn>2</mn> </mrow> <mo>⏟</mo> </munder> <mn>3</mn> </munder> </math> | 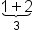 |
| \overbrace{\underbrace{1+2}_3+3}^5 (1) | <math> <mover> <mover> <mrow> <munder> <munder> <mrow> <mn>1</mn> <mo>+</mo> <mn>2</mn> </mrow> <mo>⏟</mo> </munder> <mn>3</mn> </munder> <mo>+</mo> <mn>3</mn> </mrow> <mo>⏞</mo> </mover> <mn>5</mn> </mover> </math> | 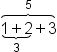 |
| Decorations | ||
| \left\langle\frac12\right\rangle | <math> <mfenced close=">" open="<"> <mfrac> <mn>1</mn> <mn>2</mn> </mfrac> </mfenced> </math> | 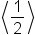 |
| {\textstyle\frac43}=1'\overset\frown3 | <math> <mstyle displaystyle="false"> <mfrac> <mn>4</mn> <mn>3</mn> </mfrac> </mstyle> <mo>=</mo> <mn>1</mn> <mo>'</mo> <mover> <mn>3</mn> <mo>⏜</mo> </mover> </math> | 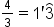 |
| \overrightarrow u+\overrightarrow v | <math> <mover> <mi>u</mi> <mo>→</mo> </mover> <mo>+</mo> <mover> <mi>v</mi> <mo>→</mo> </mover> </math> | 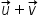 |
| \overline{x+\overline y} | <math> <mover> <mrow> <mi>x</mi> <mo>+</mo> <mover> <mi>y</mi> <mo>¯</mo> </mover> </mrow> <mo>¯</mo> </mover> </math> | 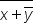 |
| x^\boxed5-x^2+\boxed3 (1) | <math> <msup> <mi>x</mi> <menclose notation="circle"> <mn>5</mn> </menclose> </msup> <mo>-</mo> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>+</mo> <menclose notation="box"> <mn>3</mn> </menclose> </math> | 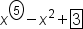 |
| \frac{a\cdot{\color[rgb]{1.0, 0.0, 0.0} \cancel{\color[rgb]{0.1, 0.1, 0.1}b}} \cdot{\color[rgb]{0.0, 0.0, 1.0} \bcancel{\color[rgb]{0.1, 0.1, 0.1}d}} \cdot{\color[rgb]{0.0, 0.5, 0.0} \bcancel{ \color[rgb]{0.1, 0.1, 0.1}e}}}{{ \color[rgb]{1.0, 0.0, 0.0}\cancel{ \color[rgb]{0.1, 0.1, 0.1}b}}\cdot c \cdot{\color[rgb]{0.0, 0.0, 1.0} \bcancel{\color[rgb]{0.1, 0.1, 0.1}d}} \cdot f\cdot{\color[rgb]{0.0, 0.5, 0.0} \bcancel{\color[rgb]{0.1, 0.1, 0.1}e}}} (1) | <math> <mfrac> <mrow> <mi>a</mi> <mo>·</mo> <menclose mathcolor="#FF0000" notation="updiagonalstrike"> <mi mathcolor="#191919">b</mi> </menclose> <mo>·</mo> <menclose mathcolor="#0000FF" notation="downdiagonalstrike"> <mi mathcolor="#191919">d</mi> </menclose> <mo>·</mo> <menclose mathcolor="#007F00" notation="verticalstrike"> <mi mathcolor="#191919">e</mi> </menclose> </mrow> <mrow> <menclose mathcolor="#FF0000" notation="updiagonalstrike"> <mi mathcolor="#191919">b</mi> </menclose> <mo>·</mo> <mi>c</mi> <mo>·</mo> <menclose mathcolor="#0000FF" notation="downdiagonalstrike"> <mi mathcolor="#191919">d</mi> </menclose> <mo>·</mo> <mi>f</mi> <mo>·</mo> <menclose mathcolor="#007F00" notation="verticalstrike"> <mi mathcolor="#191919">e</mi> </menclose> </mrow> </mfrac> </math> |  |
| Big operators | ||
| \sum_{i=1}^n2^i | <math> <munderover> <mo>∑</mo> <mrow> <mi>i</mi> <mo>=</mo> <mn>1</mn> </mrow> <mi>n</mi> </munderover> <msup> <mn>2</mn> <mi>i</mi> </msup> </math> | 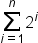 |
| \underset{q(\beta)=0}{\prod_{p( \alpha)=0}}(\alpha-\beta) | <math> <munder> <munder> <mo>∏</mo> <mrow> <mi>p</mi> <mo>(</mo> <mi>α</mi> <mo>)</mo> <mo>=</mo> <mn>0</mn> </mrow> </munder> <mrow> <mi>q</mi> <mo>(</mo> <mi>β</mi> <mo>)</mo> <mo>=</mo> <mn>0</mn> </mrow> </munder> <mo>(</mo> <mi>α</mi> <mo>-</mo> <mi>β</mi> <mo>)</mo> </math> | 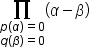 |
| \sum\nolimits_{i=1}^\infty\frac1{i^2} | <math> <msubsup> <mo>∑</mo> <mrow> <mi>i</mi> <mo>=</mo> <mn>1</mn> </mrow> <mo>∞</mo> </msubsup> <mfrac> <mn>1</mn> <msup> <mi>i</mi> <mn>2</mn> </msup> </mfrac> </math> | 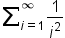 |
| \bigcap_{x\in A}A | <math> <munder> <mo largeop="true">∩</mo> <mrow> <mi>x</mi> <mo>∈</mo> <mi>A</mi> </mrow> </munder> <mi>A</mi> </math> | 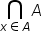 |
| Calculus | ||
| \int_0^1x^2-2dx | <math> <msubsup> <mo>∫</mo> <mn>0</mn> <mn>1</mn> </msubsup> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>-</mo> <mn>2</mn> <mi>d</mi> <mi>x</mi> </math> | 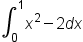 |
| \int_wdf=\int_{\partial w}f | <math> <msub> <mo>∫</mo> <mi>w</mi> </msub> <mi>d</mi> <mi>f</mi> <mo>=</mo> <msub> <mo>∫</mo> <mrow> <mo>∂</mo> <mi>w</mi> </mrow> </msub> <mi>f</mi> </math> | 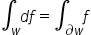 |
| \frac{\partial^2f}{\partial x\partial y} | <math> <mfrac> <mrow> <msup> <mo>∂</mo> <mn>2</mn> </msup> <mi>f</mi> </mrow> <mrow> <mo>∂</mo> <mi>x</mi> <mo>∂</mo> <mi>y</mi> </mrow> </mfrac> </math> | 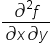 |
| \frac{d\sin(x)}{dx}=-\cos(x) (1) | <math> <mfrac> <mrow> <mi>d</mi> <mi mathvariant="normal">sin</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </mrow> <mrow> <mi>d</mi> <mi>x</mi> </mrow> </mfrac> <mo>=</mo> <mo>-</mo> <mi mathvariant="normal">cos</mi> <mo>(</mo> <mi>x</mi> <mo>)</mo> </math> | 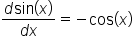 |
| \lim_{n\rightarrow\infty}\left(1+\frac1n \right)^n (1) | <math> <munder> <mi mathvariant="normal">lim</mi> <mrow> <mi>n</mi> <mo>→</mo> <mo>∞</mo> </mrow> </munder> <msup> <mfenced> <mrow> <mn>1</mn> <mo>+</mo> <mfrac> <mn>1</mn> <mi>n</mi> </mfrac> </mrow> </mfenced> <mi>n</mi> </msup> </math> | 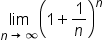 |
| \lim_{x\nearrow a}\;f(a) (1) | <math> <munder> <mi mathvariant="normal">lim</mi> <mrow> <mi>x</mi> <mo>↗</mo> <mi>a</mi> </mrow> </munder> <mo> </mo> <mi>f</mi> <mo>(</mo> <mi>a</mi> <mo>)</mo> </math> | 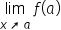 |
| \triangle u=u_{xx}+u_{yy}+u_{zz} | <math> <mo>∆</mo> <mi>u</mi> <mo>=</mo> <msub> <mi>u</mi> <mrow> <mi>x</mi> <mi>x</mi> </mrow> </msub> <mo>+</mo> <msub> <mi>u</mi> <mrow> <mi>y</mi> <mi>y</mi> </mrow> </msub> <mo>+</mo> <msub> <mi>u</mi> <mrow> <mi>z</mi> <mi>z</mi> </mrow> </msub> </math> | 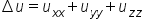 |
| \oint_{x^2+y^2=r}g(x,y)dx+h(x,y)dy | <math> <msub> <mo>∮</mo> <mrow> <msup> <mi>x</mi> <mn>2</mn> </msup> <mo>+</mo> <msup> <mi>y</mi> <mn>2</mn> </msup> <mo>=</mo> <mi>r</mi> </mrow> </msub> <mi>g</mi> <mo>(</mo> <mi>x</mi> <mo>,</mo> <mi>y</mi> <mo>)</mo> <mi>d</mi> <mi>x</mi> <mo>+</mo> <mi>h</mi> <mo>(</mo> <mi>x</mi> <mo>,</mo> <mi>y</mi> <mo>)</mo> <mi>d</mi> <mi>y</mi> </math> | 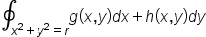 |
| Elementary | ||
| error: Error converting from MathML to LaTeX (1) | <math> <mstack charalign="center" stackalign="right"> <mscarries> <mn>1</mn> <none></none> </mscarries> <mn>35</mn> <msrow> <mo>+</mo> <mn>89</mn> </msrow> <msline></msline> <mn>124</mn> </mstack> </math> | 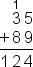 |
| error: Error converting from MathML to LaTeX (1) | <math> <mstack charalign="center" stackalign="right"> <mscarries> <mn>1</mn> <none></none> </mscarries> <mn>24</mn> <msrow> <mo>×</mo> <mn>23</mn> </msrow> <msline></msline> <mscarries> <mn>1</mn> <none></none> <none></none> </mscarries> <mn>72</mn> <msrow> <mn>48</mn> <none></none> </msrow> <msline></msline> <mn>552</mn> </mstack> <mspace linebreak="newline"></mspace> </math> | 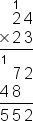 |
| error: Error converting from MathML to LaTeX (1) | <math> <mlongdiv charalign="center" charspacing="0px" stackalign="left"> <mstack charalign="center" stackalign="right"> <mn>5</mn> </mstack> <mn>69</mn> <msgroup> <msrow> <none></none> <mn>346</mn> </msrow> <msrow> <mo>-</mo> <mn>30</mn> </msrow> <msline length="3"></msline> <msrow> <none></none> <none></none> <mn>46</mn> </msrow> <msrow> <none></none> <mo>-</mo> <mn>45</mn> </msrow> <msline length="3" position="1"></msline> <msrow> <none></none> <none></none> <none></none> <mn>1</mn> </msrow> </msgroup> </mlongdiv> <mspace linebreak="newline"></mspace> </math> | 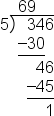 |
| error: Error converting from MathML to LaTeX (1) | <math> <mlongdiv charalign="center" charspacing="0px" longdivstyle="shortstackedrightright" stackalign="left"> <mn>7</mn> <mn>17</mn> <msgroup> <mn>123</mn> <msrow> <mo>-</mo> <mn>7</mn> </msrow> <msline length="2"></msline> <msrow> <none></none> <mn>53</mn> </msrow> <msrow> <mo>-</mo> <mn>49</mn> </msrow> <msline></msline> <msrow> <none></none> <none></none> <mn>4</mn> </msrow> </msgroup> </mlongdiv> <mspace linebreak="newline"></mspace> </math> | 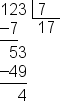 |